تبدیل داده‌های خام و کمی به اطلاعات سازمان‌یافته و مفید نیاز به قدرت ذهنی بسیار و درک بالایی دارد. درست است که همه نمی‌توانند مانند آریابهاتا، نخستین ریاضی‌دان و منجم دوره کلاسیک و اهل هند باشند، اما می‌توان با سخت‌کوشی، تمرکز و پشتکار به نتیجه مطلوب رسید.

            اکنون نوبت آن فرا رسیده است که پشتکار و سخت‌کوشی خود را برای آموختن ریاضیات و آمار و استفاده از آنها در علم داده‌ها نشان دهید.

            ریاضیات و آمار دو مورد از مهم‌ترین مفاهیم در علم داده‌ها هستند. علم داده‌ها در واقع حول این دو موضوع می‌چرخد و این مفاهیم را در کار بر روی داده‌ها از نو تعریف می‌کند. در اینجا مفاهیم مختلفی را بررسی می‌کنیم که در مجموع علم داده‌ها را شکل می‌دهند و استفاده عملی آنها را در این حوزه نشان می‌دهیم.

ریاضیات و آمار در علم داده‌ها

علم داده‌ها امروزه به یک فناوری پرطرفدار در جهان تبدیل شده است. برای یادگیری علم داده‌ها باید دانش خود را در زمینه ریاضیات و آمار تقویت کنید. پس نخست به این پرسش می‌پردازیم که ریاضیات تا چه حد در علم داده‌ها اهمیت دارد.

ریاضیات در علم داده‌ها

ریاضیات بر هر حوزه‌ای تأثیر خود را می‌گذارد. میزان استفاده از ریاضیات در رشته‌های مختلف یکسان نیست. دو جز اصلی ریاضیات که در علم داده‌ها مورد استفاده قرار می‌گیرند عبارت‌اند از جبر خطی و حساب دیفرانسیل و انتگرال.

            در مورد این دو حوزه ریاضیات که به علم داده‌ها کمک می‌کنند، به‌طور خلاصه به معرفی هر یک و تأثیر و نحوه استفاده از آنها در علم داده‌ها می‌پردازیم.

جبر خطی

جبر خطی نخستین و مهم‌ترین موضوع در علم داده‌ها است. جبر خطی به‌طور گسترده در تشخیص تصاویر، تجزیه و تحلیل متن و همچنین کاهش ابعاد مؤثر است. به این دو تصویر نگاه کنید:

می‌توانید بگویید کدام یک تصویر گربه است و کدام یک تصویر سگ؟ البته که می‌توانید. این توانایی به این دلیل در شما هست که از بدو تولد ذهن شما برای تشخیص گربه از سگ آموزش دیده است. در نتیجه می‌توانید به استفاده از غریزه خود داده‌های مختلف را به ادراکات تبدیل کنید.

            اما اگر از شما خواسته شود الگوریتمی طراحی کنید که از طریق آن بتوان گربه‌ها و سگ‌ها را از هم جدا کرد چه می‌کنید؟ به این کار «طبقه‌بندی» می‌گویند و مهم‌ترین کاربرد حوزه یادگیری ماشینی محسوب می‌شود. در واقع رایانه قادر است به کمک جبر خطی تصویر گربه را از تصویر سگ تشخیص دهد.  

            رایانه این تصویر را به شکل «ماتریس» ذخیره می‌کند. ماتریس‌ها مهم‌ترین بخش جبر خطی هستند. اساساً جبر خطی برای حل مسائل معادلات خطی طراحی شده است. این معادلات گاه شامل متغیرهایی با ابعاد بالاتر می‌شوند.

            این متغیرهای با ابعاد بالاتر را نمی‌توان به تجسم درآورد یا دستکاری کرد. از این رو ما از قدرت ماتریس‌ها استفاده می‌کنیم تا بتوانیم داده‌هایی دارای ابعاد n را دستکاری کنیم. سه نوع ماتریس وجود دارد:

یک. بردارها (Vectors) که ماتریس‌های یک‌بعدی هستند. منظور از یک‌بعدی این است که این ماتریس‌ها n ردیف اما تنها یک ستون دارند.

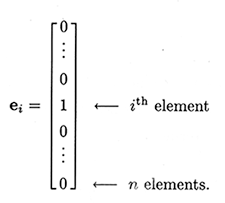
دو. ماتریس‌های دوبعدی که معروف‌ترین نوع ماتریس و دارای دو بعد هستند. در این ماتریس‌ها n ردیف و n ستون وجود دارد.

سه. اسکالرها که در آن تمام عضوهای قطر اصلی ماتریس با هم برابرند.

چندین مجموعه ابزار پشتیبانی برای جبر خطی وجود دارد. یکی از این مجموعه‌ها numpy نام دارد که در برنامه‌نویسی پایتون (Python programming) از آن استفاده می‌شود. در اینجا یک نمونه کد numpy را می‌آوریم که برای ساختن بردارها و ماتریس‌ها از آن استفاده می‌شود.

import numpy as np

arr = np.array([1,4,7,8])

arr

> array([1, 4, 7, 8])

arr2 = np.array([[1,2,3], [4,5,6], [7,8,9], [10,11,12]])

arr2

>array([[ 1, 2, 3],

[ 4, 5, 6],

[ 7, 8, 9],

[10, 11, 12]])

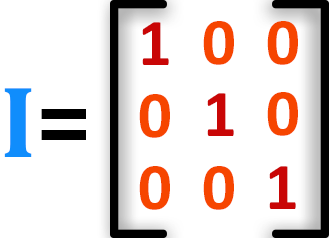
چهار. ماتریس مهم دیگری نیز وجود دارد که به آن «ماتریس هویت» (identity matrix) می‌گویند. در این ماتریس که از صفرها و یک‌ها ساخته شده است، یک‌ها مورب و سایر مقادیر ماتریس صفر هستند.

تکنیک‌های جبر خطی در علم داده‌ها

انواع دیگری از ماتریس نیز وجود دارند که در نوع خود مهم هستند، مانند ماتریس معکوس و اعمالی مانند جابه‌جایی یک ماتریس نیز شایان یادگیری هستند. حال به برخی تکنیک‌های مهم جبر خطی می‌پردازیم که در علم داده‌ها مورد استفاده قرار می‌گیرند.

تجزیه تک‌ارزشی

تجزیه تک‌ارزشی ماتریس به شما امکان می‌دهد ماتریس‌ را با تقسیم آن به سه ماتریس مختلف دستکاری کنید. این ماتریس‌ها حاصل مقیاس‌گذاری، چرخاندن و بریدن ماتریس‌های دیگر هستند.

تجزیه‌ویژه یک ماتریس

تجزیه‌ویژه یک ماتریس به شما امکان می‌دهد ماتریس‌ها را کاهش دهید تا عملیات روی ماتریس‌ها سریع‌تر انجام شود. این کار باعث ایجاد بردارهای جدید می‌شود که در همان جهت بردارهای قبلی باشند. سپس ماتریس را به مقادیر ویژه و بردارهای ویژه تجزیه می‌کنیم.

تحلیل اجزای اصلی

برای کاهش ابعاد بالاتر، از تحلیل اجزای اصلی استفاده می‌کنیم. این عملیات به‌طور گسترده برای کاهش ابعاد ماتریس مورد استفاده قرار می‌گیرد که فرایند کاهش تعداد متغیرها یا ابعاد ماتریس بدون از دست رفتن برچسب‌های همبسته ماتریس است.

حساب دیفرانسیل و انتگرال

یکی دیگر از بخش‌های ریاضیات که در علم داده‌ها مورد نیاز است، حساب دیفرانسیل و انتگرال است. حساب دیفرانسیل و انتگرال اساساً در تکنیک‌های بهینه‌سازی مورد استفاده قرار می‌گیرد. بدون حساب دیفرانسیل و انتگرال نمی‌توانید به دانشی عمیق در مورد یادگیری ماشینی دست بیابید.

            با استفاده از حساب دیفرانسیل و انتگرال می‌توان شبکه‌های عصبی مصنوعی را مدل‌سازی کرد و همچنین دقت و کارایی آنها را افزایش داد. حساب دیفرانسیل و انتگرال را می‌توان به دو دسته زیر تقسیم‌بندی کرد.

حساب دیفرانسیل

حساب دیفرانسیل سرعت تغییر کمیت‌ها را بررسی می‌کند. از مشتق بیشتر برای یافتن ماکزیمم و مینیمم توابع استفاده می‌شود. از این رو از مشتق در تکنیک‌های بهینه‌سازی استفاده می‌شود که در آنها باید مینیمم را پیدا کنیم تا بتوانیم تابع خطا را به حداقل برسانیم.

مفهوم مهم دیگری در مورد مشتق که باید بشناسید، مشتق جزئی است که برای طراحی «انتشار معکوس» (Backpropagation) در شبکه‌های عصبی به کار می‌ود. «قانون زنجیره‌ای» (Chain Rule) مفهوم مهم دیگری است که در محاسبه انتشار معکوس مورد استفاده قرار می‌گیرد.

علاوه بر به حداقل رساندن توابع خطا و انتشار معکوس، از نظریه بازی دیفرانسیل در شبکه‌های عصبی متخاصم مولد (Generative Adversarial Neural Networks) نیز استفاده می‌شود.

حساب انتگرال

حساب انتگرال مطالعه ریاضی در مورد جمع مقادیر و یافتن مساحت زیر منحنی است. انتگرال‌ها به انتگرال‌های معین و نامعین تقسیم می‌شوند.

            انتگرال‌گیری بیشتر در محاسبه توابع احتمال و اختلاف متغیرهای تصادفی مورد استفاده است. استنباط بیزی (Bayesian Inference) حوزه مهم دیگری در یادگیری ماشینی است که در آن از حساب انتگرال استفاده می‌شود.

            پس از درک مباحث مهم ریاضیات، حال باید نگاهی بیندازیم به مفاهیم مهم در حوزه آمار که در علم داده‌ها مورد استفاده قرار می‌گیرند.

آمار در علم داده‌ها

آمار یعنی پژوهشی که به جمع‌آوری،‌ تجزیه و تحلیل، تجسم و تفسیر داده‌ها می‌پردازد. علم داده‌ها مانند یک ماشین اسپرت قوی است که با آمار کار می‌کند. این ماشین از آمار برای تبدیل داده‌های خام به تعاریف و ایده‌هایی استفاده می‌کند که محصولات آن داده‌ها محسوب می‌شوند.

            آمار با داده‌های خام سروکار دارد و به صنایع کمک می‌کند تصمیمات دقیق مبتنی بر اطلاعات موثق بگیرند. علم آمار ابزارها و امکانات مختلفی در اختیار شما قرار می‌دهد که کمک می‌کند حجم بسیار بزرگی از داده‌ها را تحلیل و از آنها نتیجه‌گیری کنید.

            افزون بر این، به کمک علم آمار می‌توانید داده‌ها را خلاصه کنید و از آنها گزاره‌هایی استنتاج کنید که درک عمیقی از آن داده‌ها به شما می‌دهند. با توجه به این دو اصطلاح، می‌توان علم آمار را به دو شاخه زیر تقسیم کرد.

·       آمار توصیفی

·       آمار استنتاجی

آمار توصیفی

برای توصیف داده‌ها از علم آمار توصیفی یا خلاصه‌سازی به کمک آمار استفاده می‌شود. این شاخه به خلاصه کردن کمی داده‌ها می‌پردازد. این فرایند خلاصه‌سازی از طریق نمودارها و نمایش‌های عددی انجام می‌شود.

            به منظور درک کامل‌تر آمار توصیفی، باید مفاهیم کلیدی زیر را بشناسید.

توزیع نرمال

در توزیع نرمال یا بهنجار تعداد بسیاری از داده‌ها را در یک نمودار نشان می‌دهند. با استفاده از توزیع نرمال، مقادیر زیادی از متغیرها در یک منحنی گاوسی (Gaussian Curve) نشان داده می‌شوند.

            منحنی گاوسی ماهیتی متقارن دارد، یعنی مقادیر دورتر از حد میانگین، به‌طور مساوی در هر دو جهت در چپ و راست کاهش می‌یابند. برای انجام محاسبات در آمار استنتاجی، لازم است داده‌ها به‌صورت نرمال توزیع شده باشند.

شاخص‌ مرکزی

با استفاده از شاخص‌های مرکزی (Central tendency) می‌توانیم نقطه مرکزی داده‌ها را شناسایی کنیم. میانگین، میانه و حالت، سه بخش مهم شاخص مرکزی هستند. میانگین یعنی حد وسط همه مقادیر در داده‌های نمونه، میانه یعنی مقدار متوسط داده‌هایی که به‌صورت صعودی مرتب شده باشند و حالت، بیشترین مقدار در داده نمونه است.

خمیدگی و کشیدگی

ممکن است در نمونه‌های داده توزیع شما هیچ نوع تقارنی را نشان ندهد. مثلاً منحنی گاوسی دارای خمیدگی یا چولگی (Skewness) صفر است. وقتی داده‌های بیشتر در سمت چپ نمودار جمع شوند، شاهد شیب مثبت نمودار هستیم و وقتی داده‌ها در سمت راست جمع شوند، شیب منفی داریم.

            کشیدگی (Kurtosis) دنباله یا «دم» نمودار را اندازه‌گیری می‌کند. از دنباله‌دار بودن نمودار استنباط می‌شود که کشیدگی نمودار، مقادیر حداکثری در هر دو دنباله نمودار را اندازه‌گیری می‌کند.

            اساساً توزیع‌هایی با کشیدگی زیاد دنباله‌هایی بزرگ‌تر از توزیع‌های نرمال دارند، در حالی که کشیدگی منفی نشان‌دهنده دنباله کوچک‌تری نسبت به توزیع‌های نرمال است.

تغییرپذیری

تغییرپذیری (Variability) نشان‌دهنده فاصله بین دو نقطه داده از میانگین مرکزی توزیع است. معیارهای مختلفی برای تغییرپذیری وجود دارد، مانند دامنه، واریانس،‌ انحراف استاندارد و دامنه بین چارکی (inter-quartile ranges).

آمار استنباطی

آمار استنباطی (Inferential Statistics) روش استنباط یا نتیجه‌گیری از داده‌هاست. از طریق آمار استنباطی با انجام آزمایش و نتیجه‌گیری از نمونه‌های کوچک‌تر می‌توانیم در مورد نمونه‌های آماری بزرگ‌تر نتیجه‌گیری کنیم.

            برای نمونه در جریان نظرسنجی انتخاباتی اگر بخواهید بدانیم چند نفر از یک حزب سیاسی خاص حمایت می‌کنند، چطور این کار را انجام می‌دهید؟ آیا می‌توانید نظر تک‌تک افراد را بپرسید؟

            این رویکرد قطعاً درست نیست، زیرا مثلاً در هند بیش از یک میلیارد نفر زندگی می‌کنند و پرسیدن نظر تک‌تک آنها کاری بیش از حد دشوار است. در نتیجه نمونه‌ آماری کوچک‌تری انتخاب و براساس آن نمونه استنباط می‌کنیم و مشاهدات خود را به جمعیت بزرگ‌تر نسبت می‌دهیم.

            تکنیک‌های مختلفی در حوزه آمار استنباطی وجود دارد که در علم داده‌ها می‌توان از آنها استفاده کرد. در ادامه برخی از این تکنیک‌ها را مرور می‌کنیم.

قضیه حد مرکزی

در یک قضیه حد مرکزی (Central Limit Theorem) میانگین نمونه آماری کوچک‌تر با میانگین نمونه آماری بزرگ‌تر یکسان است. از این رو انحراف معیار (standard deviation) برابر با انحراف معیار جامعه بزرگ‌تر است.

آزمون فرضی آماری

آزمون فرضی (Hypothesis Testing) معیار سنجش یک فرضیه است. با استفاده از آزمون فرضی می‌توان نتایج حاصل از یک نمونه آماری کوچک‌تر را به یک گروه بسیار بزرگ‌تر تعمیم داد. دو فرض وجود دارد که لازم است آنها را در تقابل با یکدیگر آزمایش کنیم: یکی فرض صفر (Null Hypothesis) و دیگری فرض جایگزین (Alternate Hypothesis).

            فرض صفر نشان‌دهنده سناریوی ایده‌آل است، در حالی که فرض جایگزین اغلب برعکس آن است و با استفاده از فرض صفر سعی می‌کنیم اشتباه بودن آن را اثبات کنیم.

تحلیل واریانس

به کمک تحلیل واریانس یا Analysis of variance  که به آن ANOVA نیز می‌گویند، فرضیه‌های خود را برای گروه‌های جداگانه مورد آزمایش قرار می‌دهیم. این روش شکل بهبودیافته از یک تکنیک استنتاجی است که به آن آزمون تی گفته می‌شود. تست ANOVA با حداقل میزان خطا آزمون را انجام می‌دهد.

            یکی از معیارهای اندازه‌گیری تحلیل واریانس یا ANOVA را «نسبت اف» (f-ratio) می‌نامند. نسبت اف در واقع نسبت میانگین مربع داخلی یک گروه و میانگین مربع بین گروه‌هاست.

تحلیل کیفی داده‌ها

تحلیل کیفی داده‌ها دو تکنیک مهم دارد، یکی همبستگی (correlation) و دیگری رگرسیون (regression). همبستگی معیار یافتن روابط بین متغیرهای تصادفی و داده‌های دومتغیره است. رگرسیون نیز شکل دیگری از تحلیل کیفی داده‌هاست.

در رگرسیون روابط بین متغیرها را تخمین می‌زنیم. رگرسیون دو نوع ساده و چندمتغیره دارد. همچنین اگر تابع ماهیتی غیرخطی داشته باشد، رگرسیون نیز غیرخطی خواهد بود.

چکیده

در این مقاله در مورد نقش‌های مختلف ریاضیات و علم آمار در دانش داده‌ها و یادگیری ماشینی صحبت کردیم. نحوه استفاده گسترده از جبر خطی را در کارهای پیچیده محاسباتی و پردازشی نیز نشان دادیم. همچنین حساب دیفرانسیل و انتگرال و کاربرد آن در کاهش تابع خطا در مدل‌های آماری مورد بحث قرار گرفت. به علاوه در مورد دانش آمار گفتیم که چگونه علم داده‌ها بر آمار تکیه دارد و چگونه دو حوزه آمار توصیفی و استنتاجی هسته اصلی علم داده‌ها را شکل می‌دهند.

در نهایت به این نتیجه می‌رسیم که برای تسلط بر علم داده‌ها، دانستن ریاضیات و آمار ضروری است. درک صحیح مفاهیم حوزه ریاضیات و آمار در علم داده‌ها بسیار مهم است. به کمک آنها می‌توانید پروژه‌های مدیریت داده‌ها را به‌خوبی به سرانجام برسانید.

منبع: data-flair.training

مترجم: بهناز دهکردی